MÉTODO GRÁFICA PARA UN SISTEMA LINEAL \(\mathbf{2}\times\mathbf{2}.\)

Ahora se dirige el estudio de sistemas de ecuaciones desde el punto de vista geométrico. Se pretende llevar al letor a desarrollar las habilidades para plasmar en el plano cartesiano un sistema de ecuación, identificando así su solución de manera gráfica.

El plano cartesiano es un sistema coordenado rectangular (que forma un rectángulo), formado por dos rectas numéricas que se intersecan perpendicularmente en un punto llamado origen, correspondiente al punto cero de cada una de las rectas, mediante un sistema de coordenadas .

Las rectas numéricas horizontal y vertical son llamadas eje de abscisas (usualmente el eje \(x\)) y eje de ordenadas (usualmente eje \(y\). Los dos ejes dividen al plano en cuatro regiones llamadas cuadrantes, y no necesariamente deben tener la misma escala al ser dibujados.

El plano que queda determinado por los ejes recibe el nombre de “plano equis ye” y permite unir dos de las ramas más importante de las matemáticas, el álgebra y la geometría, las cuales siembran las bases para el estudio de otras ramas como son la trigonometría y el cálculo.

Recuerde que una recta se extiende en ambos sentidos (derecha o izquierda, arriba o abajo) hasta el infinito, sin embargo, solo se debe colocar flechas de dirección hacia la derecha y hacia arriba. Las escalas de división se toman a conveniencia de acuerdo con los valores que toman las variables del ejercicio, esto es porque el tamaño de la hoja de papel o cartulina donde escribe es limitado y la escala debe acomodarse a los datos.

Coordenadas de un punto en el plano.

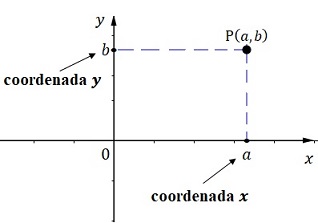Sea \(P\) un punto en el plano cartesiano, ubicado en cualquiera de los cuadrantes. Se asocia un par ordenado (pareja de números reales que tienen un orden) al punto \(P\) si se traza una recta vertical desde \(P\) al eje de abscisas (eje \(x\)) y una recta horizontal desde \(P\) al eje de ordenadas (eje \(y\).

Si la recta vertical corta el eje de abscisas en \(x=a\) y la recta horizontal corta el eje de ordenada en \(y=b\), el par ordenado de números reales asociado al punto \(P\) es \(\left(a,b\right).\) El número \(a\) es la abscisa o coordenada en \(x\) del punto y el número \(b\) es la ordenada o coordenada en \(y\). Un punto en un plano también se puede representar por el par ordenado \(\left(x,y\right)\) o \(\left(h,k\right)\) las letras a usar no importan, lo que importa es el orden.

Graficar puntos en el plano de coordenadas.

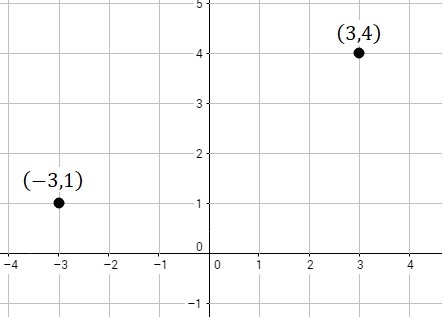Por convención se ha establecido que a la derecha y arriba del origen de coordenadas, punto \((0,0)\) es positivo, mientras que a la izquierda y abajo se considera negativo como puede verse en la figura.
Así el punto \(\left(3,\ 4\right)\) quiere decir tres unidades (lugares) a la derecha del \(\left(0,\ 0\right)\) y luego cuatro unidades hacia arriba. Para el punto \(\left(-3,\ 1\right)\) se deben considerar tres unidades a la izquierda del origen \(\left(0,0\right)\) y luego una unidad hacia arriba, como puede verse en la figura de la izquierda.

Para graficar una ecuación lineal basta conocer dos puntos por donde pasa su gráfica y unirlos con una línea recta (a sabiendas que la gráfica se extiende hasta el infinito por ambos lados). La manera más fácil de hacer esto es a través de los puntos de intersección de la recta con los ejes de coordenadas.

Interceptos o intersección con los ejes.

Se denominan interceptos con los ejes o simplemente interceptos, a los puntos de corte de la recta con los ejes de coordenadas. Para el intercepto en el eje \(x\) se hace \(y=0,\) para el intercepto en el eje ye se hace \(x=0.\)

Si en la expresión de una recta se escribe \(y=mx+n\) donde ye está despejada, se dice que la expresión está escrita en forma explícita si ye no está despejada se dice que es la forma implícita) y el intercepto en el eje ye es el punto \((0,n)\), para otro punto en la recta se hace \(x\) igual a cualquier valor y se calcula el valor de ye.

Ejemplo 1. Resolver de manera grafica el sistema $$\left\{\begin{array}13x+4y=1000\\5x-2y=800\end{array}\right.$$ Solución: determine los interceptos en cada una de las rectas y proceda a graficar. Para \(3x+4y=1000\): el intercepto en \(x,\) está para \(y=0:\)
$$3x+4\left(0\right)=1000 \Longrightarrow x=\frac{1000}{3}\Longrightarrow \ P_1\left(\frac{1000}{3},\ 0\right)$$ Intercepto en \(y,\) entonces \(x=0:\) 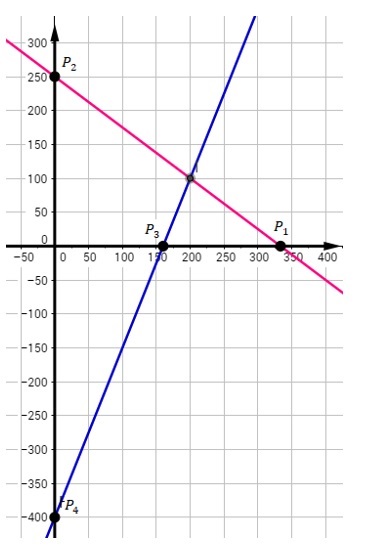$$3\left(0\right)+4y=1000\Longrightarrow y=\frac{1000}{4}=250$$ De donde se tiene el punto \(P_2\left(0,250\right)\)

Para \(5x-2y=800\)
Intercepto en \(x,\) entonces \(y=0:\) \(5x-2(0)=800\) $$x=\frac{800}{5}=160\therefore\ P_3\left(160,\ 0\right)$$ Intercepto en \(y,\) entonces \(x=0:\) \(5(0)-2y=800\)
\(y=-400~~∴ ~~P(40,-400)\)
Ahora ubique los puntos en el plano y una con una línea recta \(P_1\) con \(P_2,\) luego \(P_3\) con \(P_4,\) el punto donde las rectas se intersecan (cruzan) es el punto solución. La gráfica de arriba muestra la solución que es el punto \(P\left(200,\ 100\right).\)

Ejemplo 2. Resolver de manera grafica el sistema $$\left\{\begin{array}12x+3y=22\\7x-4y=19\end{array}\right.$$ Solución: proceda como en el ejemplo anterior para realizar la gráfica.
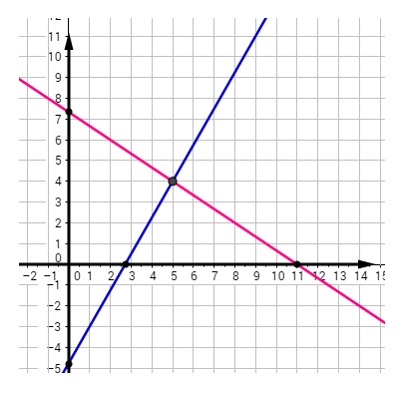Para \(2x+3y=22\) el intercepto en \(x\), hacer \(y=0\):
$$2x+3\left(0\right)=22\Longrightarrow x=11 $$ Para el punto \(P_1\left(11,\ 0\right)\)
Intercepto en \(y\), entonces hacer \(x=0.\) $$2\left(0\right)+3y=22\Longleftrightarrow y=\frac{11}{3}$$ De donde se tiene el punto \(P_2(0,\ 11/3)\)

Para la gráfica de \(7x-4y=19\) el intercepto en \(x\), está para \(y=0\):
$$7x-4(0)=19\Longleftrightarrow x=\frac{19}{5}\therefore\ P_3\left(\frac{19}{5},\ 0\right)$$ Intercepto en \(y\), entonces \(x=0:\)
\(7(0)-4y=19 ⟺ y=-19/4 \therefore P(40,-19/4)\)
Ubique ahora los puntos en el plano y una con una línea recta. La gráfica de arraiba muestra la solución que es el punto \(P\left(5,\ 4\right)\).

Note que en este ejemplo se ha elegido una escala uno a uno para los ejes mientras que en el ejemplo anterior esto no fue posible. ¿Por qué?

Ejemplo 3. Resolver de manera gráfica el sistema $$\left\{ \begin{array}1y=2x+5\\y=3x+10\end{array}\right.$$ Solución: en este ejemplo se presentan las ecuaciones de manera explícita por lo cual es muy fácil determinar los interceptos. 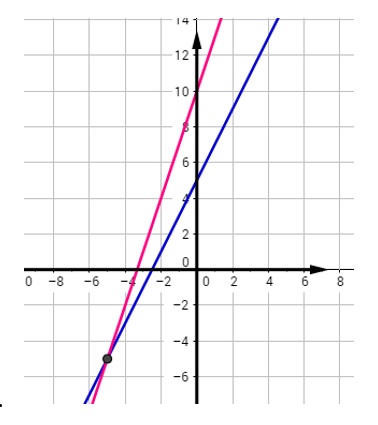Para \(y=2x+5\), el intercepto en \(y=(0,\ 5)\therefore\ P_1\left(0,\ 5\right)\)
Intercepto en \(x\), entonces hacer \(y=0:\)
\(0=2x+5\Longleftrightarrow x=-5/2\)
De donde se tiene \(P_2(-5/2,~0)\)
Para \(y=3x+10\) el intercepto en\(y\) es \(P_3\left(0,\ 10\right)\)
Intercepto en \(x,\) entonces hacer \(y=0:\) \(0=3x+10\Longleftrightarrow x=-\frac{10}{3}\)
De donde se tiene el punto \(P_4(-10/3,\ 0)\)
La gráfica muestra la solución, que es el punto \(P\left(-5,-5\ \right)\).